| 일 | 월 | 화 | 수 | 목 | 금 | 토 |
|---|---|---|---|---|---|---|
| 1 | 2 | 3 | ||||
| 4 | 5 | 6 | 7 | 8 | 9 | 10 |
| 11 | 12 | 13 | 14 | 15 | 16 | 17 |
| 18 | 19 | 20 | 21 | 22 | 23 | 24 |
| 25 | 26 | 27 | 28 | 29 | 30 | 31 |
- I'm glad
- 게임QA
- 형변환
- it's a good thing
- 명세기반테스트
- UE4
- sort함수
- relif
- Realtime Rendering
- gameQA
- ISTQB
- 제5인격
- continue to
- by any chance
- 명절 표현
- C++
- end up ing
- might have p.p
- if조건절
- java
- keep -ing
- counldn't have
- html
- know
- 코로나19
- happen to
- by until
- 변수
- for ing
- metascore
- Today
- Total
Records rather than Memories
네트워크 플로우(Network flow 본문
네트워크 플로우 알고리즘이란?
- 특정한 지점에서 다른 지점까지 데이터가 얼만큼 흐르고 있는지를 측정하는 알고리즘입니다. 좀 더 쉽게 이해하기 위해 파이프에 흐르는 물의 양을 구하는 방식이라고 설명합니다. 네트워크 플로우는 교통 체증, 물류, 네트워크 데이터 전송 등 다양한 부분에서 활용 될 수 있습니다.

리니지라는 게임에 나오는 마을과 사냥터를 가정해 생각해보자.
말하는 섬에서 폐허의 땅이라는 사냥터까지 가는 길의 폭이 10, 폐어의 땅에서 아덴대륙 가는길의 폭이 5라고 가정해보자. 한 사람이 말하는 섬에서 아덴대륙까지 가는데 1시간이 걸린다면 10명의 사람을 한번에 말하는 섬에서 아덴대륙까지 보낸다면?

다음과 같이 폐허의 땅에서 아덴대륙으로 갈 수 있는 양은 3명이므로 2명은 폐허의 땅에 남게된다.
따라서 막힘없이 말하는 섬에서 아덴 대륙으로 보내기 위해서는 1시간에 3명씩 보내야 한다.
이 것을 3/8과 3/3으로 표현할 수 있는데 유량 / 용량으로 표현하는 방식이다.

네트워크 플로우를 확인해보자. 각각의 용량(Capacity)와 유량(Flow)를 하나의 간선으로 표현했다. 여기서 실질적인 문제인 A에서 D까지 최대한 많은 유량을 보내려고 할 때 가장 알맞은 양 즉 가장 많은 양은 얼마일까?
답은 바로 6이다. B에서 C까지 가능한 용량이 6으로 가장 적기때문에 정체가 발생하지 않는 최대의 유량이 되게 된다.

이번엔 눈으로 계산할 수 없는 복잡한 상황에서 A부터 F까지 갈 수 있는 최대 유량을 계산해보자. 기본적으로 네트워크 플로우를 구하기 위해 BFS(너비 우선 탐색) 알고리즘을 이용한다. 이것을 에드몬드 카프(Edomonds-Karp)라고 하는데 실제로 한번 적용해보자.
가능한 모든 경로를 탐색하고 정해진 용량에서 가능한 용량의 양을 반복적으로 더해주면 된다.

가장 첫 번째로 A - B - C - F 로 가는 경로가 존재한다.
경로에서 최소 유량은 6이므로 6만큼 경로에 모두 흘려보내준다는 의미로 6을 더해준다.

그다음으로 A - B - F 로 가는 경로가 존재한다.
여기서 흐를 수 있는 최소 유량이 6이므로 모두 6씩 더해주고 이 과정에서 A - B로 가는 유량이 모두 차게 된다.
중요한 것은 어느 경로든 순서 상관없이 가능한 유량을 더해주기만 하면 되므로 매우 편리하다.

A - D - E - F 경로에서도 최소 유량 4를 더해준다.
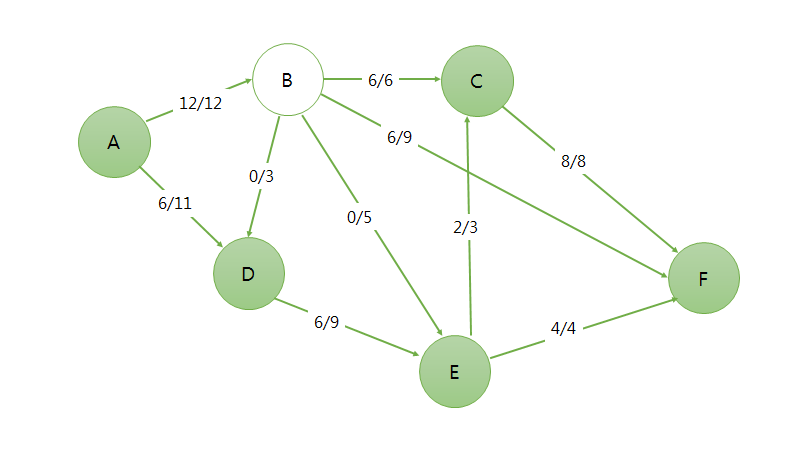
A - D - E - C - F 경로에서도 C - F에 남은 유량이 2밖에 없다.
여기까지 하면 네트워크 플로우의 알고리즘이 모두 끝났다. 가 아니라!!!
핵심적인 부분이 등장하게 된다. 바로 음의 유량을 가정하고 계산해 가능한 모든 경로를 다 계산해준다.
우리가 유량을 더해주는 과정에서 보이지 않게 반대로 가는 유량이 빠지고 있다는 것이다.

이해가 잘 되지 않을텐데 B - C로 흐르는 유량을 살펴보자. 6만큼 B에서 C만큼 흐르고 있다는 사실은 반대로 C에서 B만큼 흐르고 있다고 볼 수 있다. 불가능한 이야기지만 남아있는 모든 경로를 찾기 위해 적용한다. 따라서 용량은 6 유량은 -6으로 기록이 된다.

이러한 음의 유량으로 인해 A - D - E - C - B - F 라는 경로가 발견된다. 이렇게 되면 1 만큼의 유량을 더 보낼 수 있게 된다. 단 여기서 B - C로 가는 유량은 역으로 1을 빼주어야 한다.
이제는 실제로 네트워크 플로우를 구현해보자. BFS를 이용해 가능한 경로를 찾고 남은 용량만큼 유량을 흘려보내주면 된다.
|
1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
|
#include <iostream>
#include <vector>
#include <queue>
#include <algorithm>
#define MAX 100
#define INF 100000000
using namespace std;
int n = 6, result; //result는 최종적으로 구할 최대유량
int c[MAX][MAX], f[MAX][MAX], d[MAX]; //c 용량, f 유량, d 노드 방문 여부
vector<int> a[MAX];
void maxFlow(int start, int end) { //최대유량 구하는 메소드
while(1) {
fill(d, d + MAX, -1); //방문하지 않은 노드 초기화
queue<int> q;
q.push(start);
while(!q.empty()) { // BFS 수행
int x = q.front();
q.pop();
for(int i = 0; i < a[x].size(); i++){
int y = a[x][i];
// 방문하지 않은 노드 중에서 용량이 남은 것
if(c[][] - f[][] > && d[] == -1) {
q.push(y); // 방문할 수 있을 때 push
d[y] = x;
// 경로를 기억
if(y == end) break; // 도착지 도달
}
}
}
if(d[end] == -1) break; // 가능한 모든 경로를 탐색하면 반복문 탈출
int flow = INF; //최소값을 찾아해서 INF 초기화
// 거꾸로 최소 유량 탐색
for(int i = end; i != start; i = d[i]) {
flow = min(flow, c[d[i]][i] = f[d[i]][i]);
}
// 최소 유량만큼 추가
for(int i = end; i != start; i = d[i]) {
f[d[i]][i] += flow;
f[i]d[[i]] -= flow; // 음의
}
result += flow;
}
}
int main(void) {
a[1].push_back(2);
a[2].push+back(1);
c[1][2] = 12;
a[1].push_back(4);
a[4].push_back(1);
c[1][4] = 11;
a[2].push_back(3);
a[3].push_back(2);
c[2][3] = 6;
a[2].push_back(4);
a[4].push_back(2);
c[2][4] = 3;
a[2].push_back(5);
a[5].push_back(2);
c[2][5] = 5;
a[2].push_back(6);
a[6].push_back(2);
c[2][6] = 9;
a[3].push_back(6);
a[6].push_back(3);
c[3][6] = 8;
a[4].push_back(5);
a[5].push_back(4);
c[4][5] = 9;
a[5].push_back(3);
a[3].push_back(5);
c[5][3] = 3;
a[5].push_back(6);
a[6].push_back(5);
c[5][6] = 4;
maxFlow(1, 6);
printf("%d", result);
}
|
cs |
'Software > C' 카테고리의 다른 글
| [C++] cout, cin, endl (0) | 2019.12.28 |
|---|---|
| [C++] 변수의 초기화와 할당 (0) | 2019.12.28 |
| 위상 정렬(Topology Sort) (0) | 2019.12.13 |
| 플로이드 와샬(Floyd Warshal) 알고리즘 (0) | 2019.12.11 |
| 다이나믹 프로그래밍 : : 타일링 문제 (0) | 2019.12.03 |


